

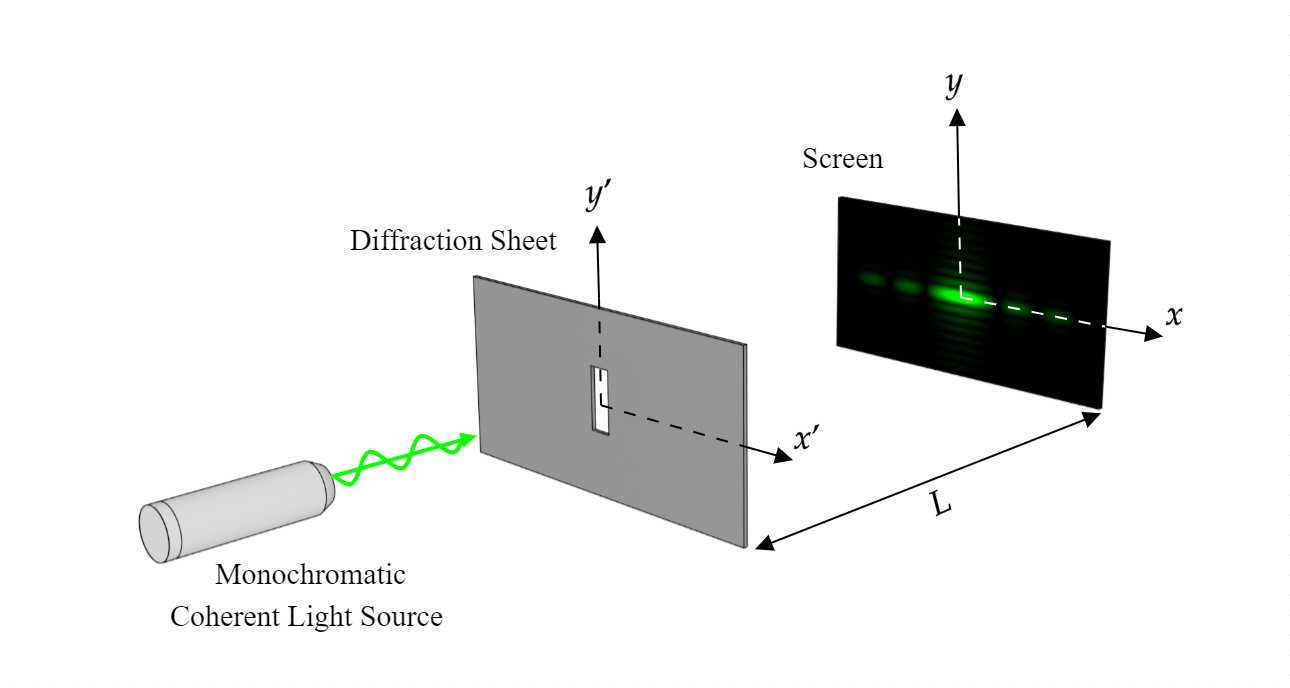
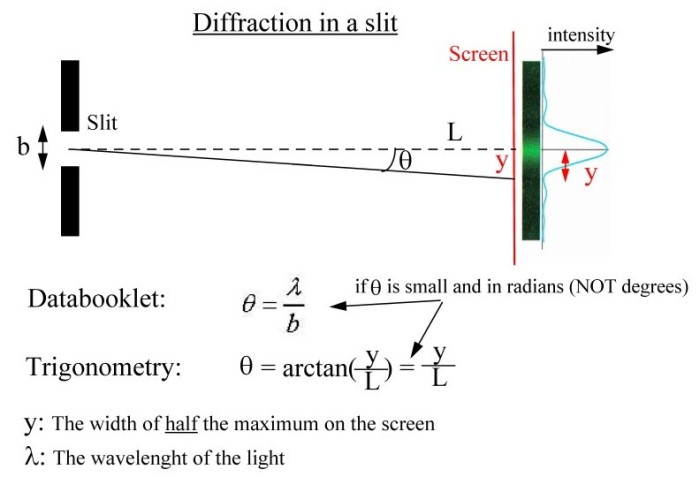
Based on this, the formula for small ϑ will be sin θ$\approx$θ. This leads to the development of the formula that is tanθ $\approx$ θ$\approx$ y/D. In such cases, the position of the minima is generally expressed by the y, and the measurement the width of which is generally measured from the centre of the screen. Based on this concept it can be explained in a simple diction that the central maximum can be referred to as the distance that lies between first-order minima from the central position of the screen that is existed on both the sides of the centre. `The position of maxima is identified in between the width and the minima of the central context (Yin, He & Wu, 2020). Therefore, the formula of the first fringe will be ΔL = λ2 = a/2sinθ where λ = a sin θ and for the second minima, the formula will be λ/2 = a/4sin θ where 2λ = a sin θ. Based on this, the formula that can be expressed mathematically isįor the dark fringe, the wavelength is calculated between λ2 and λ. Considering that, the emanation of two rays takes place at a distance of a/2 from each other. The angular position of any point on the screen that is $\mathrm$ has the measurement that is found by the centre of slit that divides the slit by the length of a/2 (, 2022). For better understanding, it is conjectured that the width of the slit is The formula of the single-slit diffraction can be represented through mathematical representation. This change observed in the frequency often produces a distinctive pattern on the screen placed behind the slit that is called the diffracted pattern. The experiment proves that the light waves have a specific wavelength and the frequency of these wavelengths can be changed when a reaction happens in the wave of light while travelling through a small slit (Qi & Wong, 2022). The bending phenomenon of light is generally observed in the experiment of Single-slit diffraction. What is single slit diffraction?įigure 1: Single-slit diffraction pattern The calculation of single-slit diffraction will be included in the tutorial. Furthermore, the tutorial will include an explanation of the formula of single-slit diffraction along with defining the central maximum as well. You then draw the line from $v_-$ to $v_+$ to get a line that represents both amplitude and phase of the wave at a given point on the screen.Ī derivation of the shape of the curve (which is a representation of the Fresnel integrals, as you correctly found) can be found here.The phenomenon of pressing waves around obstacles is commonly known by the term diffraction, based on this simple concept of physics, the present tutorial will explain the definition of a single-slit diffraction while explaining the pattern of diffraction. So I took the amplitude function (for the screen) as $A(x)$ and: Where $r$ is the distance between the point of origin on the slit and point of contact on the screen (and $k$ is the angular wave-number).
The amplitude for a wave originating from a point on the slit should be: With this function, I decided I would use the standard expression for intensity (i.e. So I decided to take the amplitudes of the waves originating from the slit on the left (wherein the variable that denotes distance within the slit is $l$) and integrate the amplitudes over the entire slit width, taking some point at a distance $x$ on the screen to achieve the resultant amplitude of the waves that strike the screen. I am trying to derive the intensity variation function for a single slit diffraction.


 0 kommentar(er)
0 kommentar(er)
